Ver. 1.0 Beta, Nie masz kompilatora? Teraz możesz pisać skrypty ONLINE! Wersja podstawowa -nie zawiera wszystkich poleceń Pascala. Służy do nauki podstaw

Jak zaprogramować zegar wskazówkowy w Turbo Pascalu. Instrukcja krok po kroku

Pascal

Wsteczwstecz Moduły
W góręw górę Podstawy Pascala
Dalejdalej Obsługa plików

Jak zaprogramować zegar wskazówkowy w Turbo Pascalu. Instrukcja krok po kroku

Zegar wskazówkowy*


Do stworzenia zegara wskazówkowego będzie potrzebna lekka umiejętność matematyki. Naszym zadaniem będzie obliczenie kątów jakie wskazówka pokonała od godziny 0:00. Będziemy zamieniali liczbę minut, które minęły od początku godziny na stopnie, a stopnie na radiany. Podobna operacja czeka nas z godziną i sekundami.


Kolejna uwaga, Twoja karta grafiki musi być zgodna ze standardem VESA. Niestety, coraz więcej firm produkujących karty graficzne, zrezygnowało z podtrzymywania tego standardu. Być może będziesz musiał programować na VirtualPC -program, na którym można emulować inny komputer.


Niżej opisany jest ogólny schemat budowy i rozwoju programu. Pomoże Ci ustalić jak w rzeczywistości powstaje bardziej skomplikowany kod. W rzeczywistości trzeba go podzielić na mniejsze punkty, co chwilę je testować i dodawać kolejne. Warto regularnie zapisywać program (F2) – przed każdym jego uruchomieniem, a nawet co napisanie kilku linii programu.



Uruchomienie grafiki

Wyłączenie grafiki

Najpierw zajmujemy się najprostszymi operacjami, w dodatku tymi, bez których dalszy kod programu nie ruszy. W tym wypadku włączeniem grafiki.




Uruchomienie grafiki
Narysowanie tarczy zegara
Wyłączenie grafiki

Później warto narysować tarczę, czyli zobaczyć pierwsze efekty swojej pracy. Tarcza będzie jeszcze bez wskazówek, ale da Tobie dużo satysfakcji... w końcu coś zaczyna się dziać.


Następnie dobrze narysować krótkie linie, ułatwiające odczytanie z tarczy minuty. Będzie ich 60, najlepiej zrobić to w pętli i pierwszy raz skorzystać w poważnej matematyki (Sinus, Cosinus). Jest 360 stopni w pełnym kole, więc co 6 stopni powinna być kolejna linia.


Ale jak za pomocą stopni ustalić pozycje 60 linii? Będziemy potrzebowali wyliczyć współrzędne x i y dla każdego punktu. Każda linia potrzebuje 2 punktów. Trzeba przypomnieć więc kilka informacji z matematyki: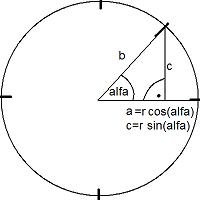


Obliczanie kąta za pomocą funkcji Sinus, Cosinus

Długość odcinka "a", czyli oddalenie wyliczanego punktu od środka liczymy ze wzoru: a = r cos ?. Długość odcinka c = r sin ?. Teraz do środka współrzędnych tarczy musimy dodać: w poziomie odcinek a, a w pionie odjąć odcinek c. Manipulując promieniem -dodając jeden odrobinę dłuższy od drugiego otrzymamy dwie współrzędne dla dwóch punktów. Możemy połączyć już je linią.


W Pascalu funkcje sinus i cosinus potrzebują wartości w radianach by wyliczyć żądaną wartość. W pełnym kole jest 360 stopni co odpowiada wartości 2? (w radianach). Z tego wynika, że



360° =  2? (rad),
1° =  2? / 360 (rad),
1° =  ? / 180 (rad),
x° odpowiada  x * (? / 180) (rad),

Aby więc wyliczyć sin 30° wpiszemy:

WriteLn Sin(30 * (PI / 180));


Co piąta minuta powinna być grubsza.


       

FOR i:=1 TO 60 DO
       BEGIN
         IF (i MOD 5<>0) THEN SetLineStyle(0, $FF, 1) ELSE SetLineStyle(0, $FF, 3);
         SetColor(7);
         Line(Sx+Round(Sin((540-i*6)*(PI/180))*(DlM+12)),
              Sy+Round(Cos((540-i*6)*(PI/180))*(DlM+12)),
              Sx+Round(Sin((540-i*6)*(PI/180))*(DlM+18)),
              Sy+Round(Cos((540-i*6)*(PI/180))*(DlM+18)));

       END;


Potrzebny jest nam promień tarczy zegara a także kąt jaki pokonała wskazówka. W matematyce kąty liczymy od poziomu w górę, w zegarze interesują nas kąty od godziny dwunastej w dół. Przy rysowaniu poruszającej się wskazówki trzeba więc uwzględnić, że ruch wskazówek zegara jest przeciwny do zwiększającego się kąta w matematyce a w dodatku nie zaczyna się od tego samego miejsca.


To jednak nie jest dla nas problemem. Wskazówka minutowa matematycznie pokonuje drogę od kąta 90 stopni, potem 84, 78, 72 aż do 0 a następnie 354, 348 itd.. aż do 90 stopni. Zamiast zwiększać kąty, będziemy je odejmować od 90. (Wskazówka minutowa porusza się kątowo wg wzoru: ? = 90 – m * 6, gdzie zmienna m to kolejna minuta od 0 do 59)


Godzina dwunasta ma kąt 90 stopni, trzecia ma kąt 0 stopni, szósta 270 a dziewiąta 180. Czyli wskazówka godzinowa występuje co 30 stopni. Z tego wzór na obliczenie kąta godziny to: ? = 90 – g * 30, gdzie g to numer godziny (od 0 do 11)


Z wartościami kątów nie będzie problemów, bo przecież rysujemy 60 razy linię co 6 stopni. Korzystając z pętli ze zmienną i od 1 do 60, będziemy po prostu mnożyli zmienną "i" przez 6. Orzymamy w wyniku 6, 12, 18, 24... 354, 360


Narysowanie tarczy zmobiluzuje Cię do dalszej pracy. Trzeba pamiętać, by dodać pętlę czekającą na naciśnięcie klawisza, żeby wogóle cokolwiek zauważyć.




Uruchomienie grafiki
Dodanie pętli aż do momentu naciśnięcia klawisza
 Narysowanie tarczy zegara
Koniec pętli
Wyłączenie grafiki

Pętla spowoduje, że program będzie się wykonywał w kółko. Zacznie od początku, dojdzie do końca i znowu zacznie od początku.



while (PORT[$60]<>1) do
   begin
     {...}
   end

Tarczę zegara i wskazówki rysujemy tylko wtedy, gdy jest to potrzebne, czyli co sekundę -gdy pozycja wskazówek ulegnie zmianie. Nie ma potrzeby, żeby tarcza się cały czas rysowała, bo będzie to obciążało procesor komputera a poza tym będzie bardzo mocno migało. Dlatego właśnie w programie jest warunek:



GetTime(h, m, s, ss);
     if (s<>sse) then
   begin
     {...}
     sse := s;
   end;

W tym wypadku zmienna sse przechowuje starą wartość sekund a zmienna 's' aktualną. Jeśli aktualna ilość sekund jest różna od starej, wtedy... rysujemy cały zegar. Oczywiście trzeba po sprawdzeniu warunku do zmiennej 'sse' przypisać wartość 's', bo teraz starą sekundą będzie ta, właśnie narysowana.


A jak narysować wskazówki? To jest znacznie prostsze od narysowania tarczy. Jeden koniec wskazówki będzie w środku koła, drugi koniec będzie ruchomy, będzie przesuwał się dookoła tarczy.



Uruchomienie grafiki
Dodanie pętli aż do momentu naciśnięcia klawisza
 Dodanie warunku -jeśli zmieniła się sekunda
 Narysowanie tarczy zegara
 Narysowanie wskazówek
Koniec pętli
Wyłączenie grafiki

Już wiemy jak obliczyć współrzędne X i Y punktu znajdującego się na okręgu o podanym promieniu, dla dowolnego kąta. Teraz wystarczy zamienić ilość minut, sekund i godzin na odpowiedni kąt i wszystko gotowe. Rysujemy trzy linie, każdą o jej własnym stylu graficznym.



Line(Sx, Sy, Sx+Round(Sin((540-m*6)*(PI/180))*DlM),
            Sy+Round(Cos((540-m*6)*(PI/180))*DlM));

Zmienna Sx, Sy oznacza tu środek tarczy zegara. 'm' to ilość minut. (540-m*6) to zamieniona ilość minut na kąt. (540-m*6)*(PI/180) to obliczenie wartości radianowej z kątowej -bo tego właśnie wymaga funkcja Sin(). Na koniec mnożymy otrzymany wynik przez DlM, czyli długość wskazówki minutowej. Jeśli zmienisz wartość DlM na mniejszą, wskazówka będzie krótsza, jeśli ułożysz nieprawidłowo obliczanie kąta, wskazówka będzie się cofać, albo zaczynać nie od minuty :00 tylko od innego miejsca.


Poniżej znajduje się całkowity kod źródłowy zegara wskazówkowego w Turbo Pascalu. Poeksperymentuj trochę z zegarem a dużo się z tego nauczysz. Będziesz wtedy dobrze wiedzieć co odpowiada za jakie właściwości i przede wszystkim łatwiej Ci będzie zrozumieć ideę tworzenia podobnych kodów.



uses Graph, Dos;

const
    Sx : Integer = 320;
    Sy : Integer = 240;

    DlM = 100;
    DlH = 80;
    DlS = 90;

    GM = 1;
    GH = 3;
    GS = 1;



var
  h, m, s, ss : Word;
  sse         : Word;
  i           : Integer;


  grDriver: Integer;
  grMode: Integer;
  ErrCode: Integer;

function IntToStr(i:Integer):string;
var s:string;
begin
 Str(i, s);
 if (i<10) then s:='0'+s;
 IntToStr:=s;
end;


begin

 grDriver :=Detect;
 InitGraph(grDriver, grMode,' ');
 ErrCode := GraphResult;
 if ErrCode = grOk then
 begin  { Do graphics }

   while (PORT[$60]<>1) do
   begin

     GetTime(h, m, s, ss);
     if (s<>sse) then
     begin
       ClearDevice;
       SetColor(10);
       OutTextXY(560, 460, IntToStr(h)+':'+IntToStr(m)+':'+IntToStr(s));
       SetColor(7);
       SetFillStyle(1, 8);
       FillEllipse(Sx, Sy, DlM+20, DlM+20);

       for i:=1 to 60 do
       begin
         if (i mod 5<>0) then SetLineStyle(0, $FF, 1) else SetLineStyle(0, $FF, 3);
         SetColor(7);
         Line(Sx+Round(Sin((540-i*6)*(PI/180))*(DlM+12)),
              Sy+Round(Cos((540-i*6)*(PI/180))*(DlM+12)),
              Sx+Round(Sin((540-i*6)*(PI/180))*(DlM+18)),
              Sy+Round(Cos((540-i*6)*(PI/180))*(DlM+18)));

       end;


       sse := s;

       SetColor(15);
       SetLineStyle(0, $FF, GH);
       Line(Sx, Sy, Sx+Round(Sin((540-h*30)*(PI/180))*DlH),
            Sy+Round(Cos((540-h*30)*(PI/180))*DlH));

       SetColor(9);
       SetLineStyle(0, $FF, GM);
       Line(Sx, Sy, Sx+Round(Sin((540-m*6)*(PI/180))*DlM),
            Sy+Round(Cos((540-m*6)*(PI/180))*DlM));

       SetColor(12);
       SetLineStyle(0, $FF, GS);
       Line(Sx, Sy, Sx+Round(Sin((540-s*6)*(PI/180))*DlS),
                    Sy+Round(Cos((540-s*6)*(PI/180))*DlS));


     end;

   end;

   CloseGraph;
 end
 else
   Writeln('Graphics error:', GraphErrorMsg(ErrCode));


end.

 
Wsteczwstecz Moduły
W góręw górę Podstawy Pascala
Dalejdalej Obsługa plików

Programy ON-LINE!

Strona korzysta z plików cookie w celu świadczenia usług Google (reklamy, statytyki) oraz Facebook. Jeśli chcesz zablokować pliki cookies wyłacz je w swojej przeglądarce. Potrzebujesz pomocy? kliknij